© 2025 Astra.si. Todos los derechos reservados.
"Para la próxima generación."
© 2025 Astra.si. Todos los derechos reservados.
"Para la próxima generación."
En el análisis matemático, uno de los conceptos clave es aquel que describe el cambio de una función con respecto al cambio en su argumento. Este concepto conduce a la definición formal de la derivada, que es la base de muchas construcciones y teorías matemáticas posteriores. La idea central es que la derivada mide la tasa de cambio de una función en un punto dado, es decir, cuán rápido y en qué dirección está cambiando la función en ese punto.
Sea 'f' cualquier función real y x₀ un punto en su dominio. La derivada de la función 'f' en el punto x₀ se denota como f′(x₀) y se define como el límite del cociente de diferencias, si este límite existe: f′(x₀) = lim (cuando h → 0) [f(x₀ + h) – f(x₀)] / h. En esta expresión, 'h' representa un pequeño cambio en la variable independiente x, mientras que el numerador muestra el cambio en el valor de la función. Si este límite existe, decimos que la función es diferenciable en ese punto.
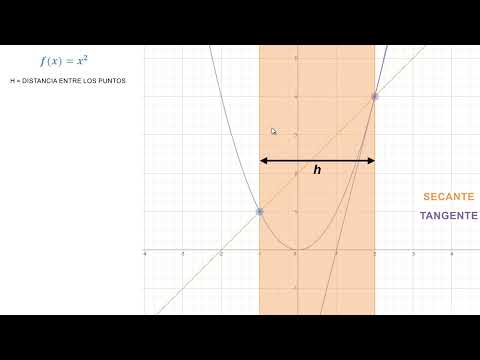
Geométricamente, la derivada representa la pendiente de la recta tangente a la gráfica de la función en el punto x₀. Si imaginamos la gráfica de la función como una curva suave, entonces la tangente en un punto dado indica la dirección en la que se dirige la curva. Cuanto mayor sea la derivada, más pronunciada será esta pendiente.
Usemos la definición:
f′(x) = lim (cuando h → 0) [(x + h)² – x²] / h
= lim (cuando h → 0) [x² + 2xh + h² – x²] / h
= lim (cuando h → 0) [2xh + h²] / h
= lim (cuando h → 0) (2x + h) = 2x.
Por lo tanto, la derivada de la función x² es 2x. Esto significa que los valores de esta función en el punto x están cambiando a una tasa de 2x.
La derivada es una herramienta matemática para describir la tasa de cambio de una función. Usando el límite del cociente de diferencias, llegamos a una definición precisa que tiene tanto un significado numérico como geométrico. Al comprender ejemplos básicos, como la función cuadrática, podemos construir más fácilmente el conocimiento sobre funciones más complejas.
¿Qué es una Derivada?
Explicación
13 minutos
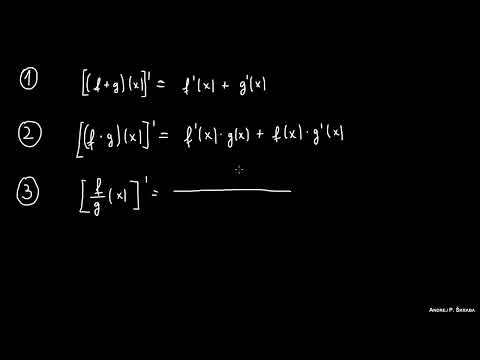
Reglas de Derivación
Explicación
4 minutos
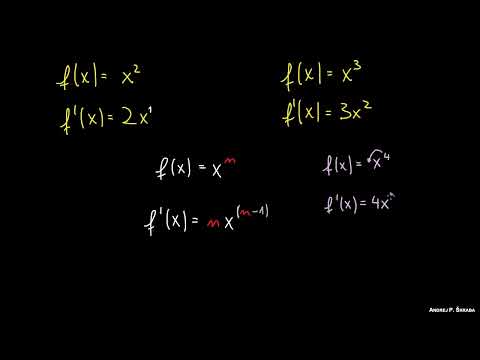
Reglas para Derivar
Explicación
5 minutos
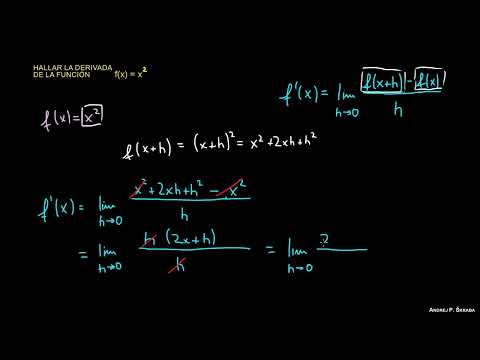
Derivada por Definición
Explicación
6 minutos
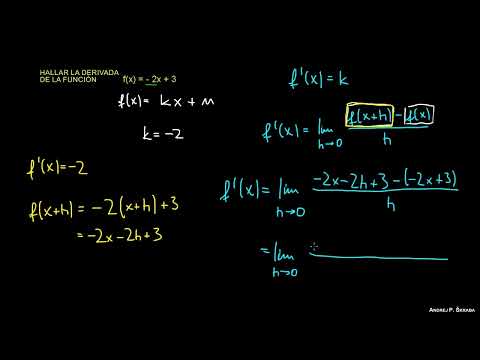
Derivada por Definición 2
Explicación
5 minutos
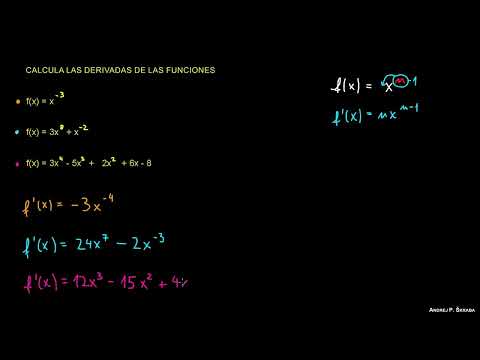
Derivadas: Ejercicio 1
Explicación
5 minutos

Derivadas: Ejercicio 2
Explicación
4 minutos
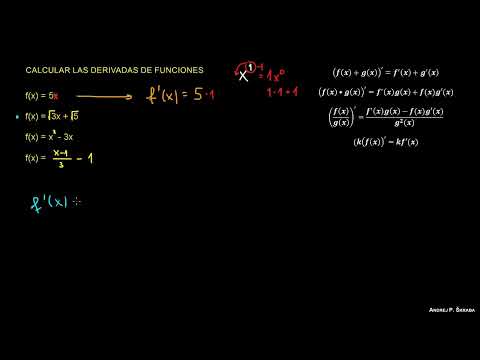
Derivadas: Ejercicio 3
Explicación
4 minutos