© 2025 Astra.si. Todos los derechos reservados.
"Para la próxima generación."
Una función cuadrática es una de las funciones más importantes en el análisis matemático, ya que describe muchos procesos naturales y físicos. La forma general de una función cuadrática es: f(x) = ax^2 + bx + c donde a, b, y c son números reales, y a no debe ser igual a cero. Esta función tiene una forma de parábola y es fundamental para entender estructuras algebraicas y análisis gráficos.
Una función cuadrática es una función de segundo grado, lo que significa que el exponente más alto de la variable x es 2. Su forma general describe una curva llamada parábola, que puede abrirse hacia arriba o hacia abajo dependiendo del valor del coeficiente a. Si a es positivo, la parábola se abre hacia arriba; si a es negativo, se abre hacia abajo. La función cuadrática es la base para estudiar otros tipos de funciones y está presente en numerosas situaciones de la vida real, como el cálculo de movimiento y la optimización.
Una función cuadrática tiene varias propiedades características que son clave para su comprensión. Una de las más importantes es el vértice de la parábola, que representa el valor mínimo o máximo de la función. El vértice es el punto donde la función alcanza su valor más alto o más bajo, dependiendo del signo del coeficiente a. Además, una función cuadrática tiene ceros (o raíces), que representan los puntos donde la gráfica de la función intersecta el eje x. Estos puntos se calculan utilizando la fórmula cuadrática.
Los ceros de la función cuadrática son cruciales para su análisis, ya que proporcionan información sobre los puntos donde la función alcanza un valor de 0. Para calcular los ceros, utilizamos la fórmula cuadrática (también llamada fórmula resolvente), que tiene la forma: x = (-b ± √(b^2 - 4ac)) / (2a) Esta fórmula permite el cálculo de los ceros basándose en los valores de los coeficientes a, b, y c. Los ceros son importantes para analizar las transiciones de la función a través de valores específicos y permiten una mejor comprensión de su estructura.
La gráfica de una función cuadrática es una parábola, que es simétrica con respecto a una línea llamada eje de simetría. Este eje pasa por el vértice de la parábola y se puede calcular con la fórmula: x = -b / (2a) El eje de simetría divide la parábola en dos partes iguales. La gráfica de una función cuadrática permite una rápida visualización de su comportamiento, lo cual es importante al analizar diversos procesos matemáticos y físicos. Con la ayuda de la gráfica, podemos identificar rápidamente dónde la función es creciente, decreciente o alcanza valores extremos.
La función cuadrática tiene una amplia aplicación en diversas disciplinas científicas. En física, se utiliza a menudo para describir el movimiento de los cuerpos en un lanzamiento vertical, donde la velocidad y la aceleración del cuerpo siguen una trayectoria parabólica. También es clave en la optimización, donde el objetivo es encontrar el valor más alto o más bajo de una cierta cantidad. Además, se utiliza en economía y estadística, donde ayuda a analizar las tendencias del mercado y predecir cambios.
La función cuadrática es uno de los conceptos fundamentales en el análisis matemático. Su forma parabólica permite un análisis preciso de funciones que describen diversos fenómenos naturales. Comprender las propiedades de una función cuadrática, como el vértice, los ceros y el eje de simetría, es crucial para analizar problemas del mundo real. Además, juega un papel importante en los análisis gráficos y permite una visualización más fácil de los problemas matemáticos. Así, la función cuadrática no es simplemente un concepto matemático, sino una herramienta que permite una comprensión más profunda del mundo que nos rodea, desde la física hasta la economía y la estadística.
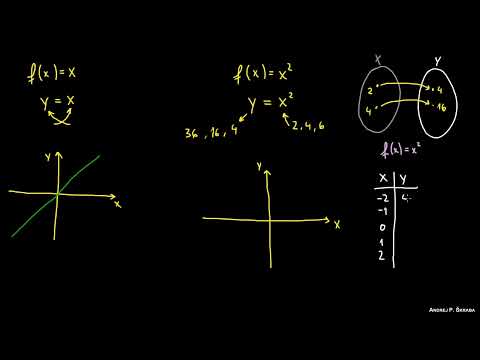
Función Cuadrática: Significado de los Coeficientes (a, b, c)
Explicación
5 minutos
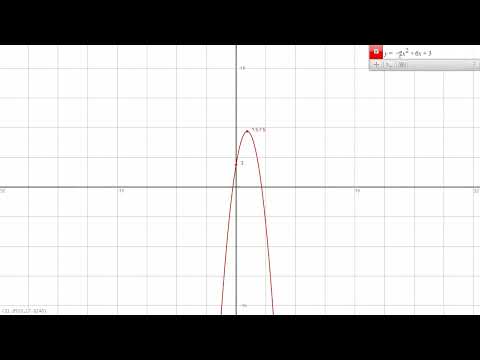
Vértice de una Parábola: Cómo Encontrarlo y su Significado
Explicación
8 minutos
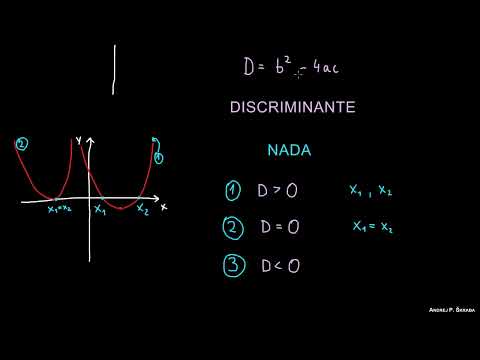
Ceros de una Función Cuadrática: Cómo Encontrarlos
Explicación
7 minutos

Graficar una Función Cuadrática: Ejemplo Paso a Paso
Explicación
9 minutos
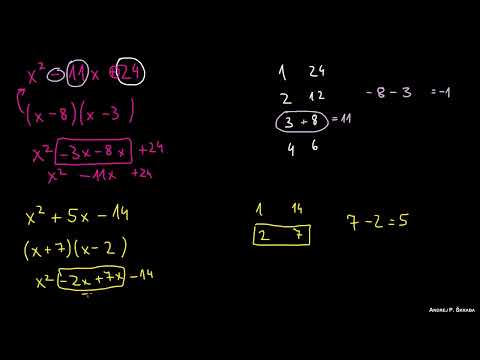
Factorización de Ecuaciones Cuadráticas: Métodos y Guía
Explicación
14 minutos